排列组合公式是数学中重要的概念,用于计算从n个不同元素中取出m个元素的所有可能组合或排列的数量。基础计算方法包括:,,1. 排列公式P(n,m)=n!/(n-m)!,表示从n个不同元素中取出m个元素进行排列的数目。,2. 组合公式C(n,m)=n!/[m!(n-m)!],表示从n个不同元素中取出m个元素进行组合的数目。,,进阶解析包括:,,1. 递推法:利用P(n,m)=P(n-1,m)+P(n-1,m-1)和C(n,m)=C(n-1,m)+C(n-1,m-1)的递推关系,计算较大规模的排列和组合问题。,2. 组合数的性质:如C(n,m)=C(n,n-m),C(n,m)=C(m,m)等,可以简化计算过程。,3. 组合恒等式:如Vandermonde恒等式,可以用于解决一些特殊的组合问题。,,掌握排列组合公式的计算方法,对于解决实际问题、提高数学思维能力具有重要意义。
在数学中,排列组合是研究如何从给定数量的元素中选取若干个元素进行排列或组合的学问,它广泛应用于统计学、计算机科学、概率论等多个领域,掌握排列组合公式的计算方法,不仅能帮助我们解决实际问题,还能在更深的层面上理解数学中的组合逻辑,本文将从基础概念出发,逐步介绍排列组合公式的计算方法,并探讨其在实际问题中的应用。
一、基础概念
1、排列(Permutation):从n个不同元素中取出m(m≤n)个元素,按照一定的顺序排成一列,称为这n个元素的一个排列,排列的个数记作P(n, m)。
2、组合(Combination):从n个不同元素中取出m(m≤n)个元素并成一组,不考虑元素的顺序,称为这n个元素的一个组合,组合的个数记作C(n, m)。
二、排列公式及其计算方法
排列公式为:P(n, m) = n! / (n - m)!,!”表示阶乘,即n! = n × (n-1) × ... × 2 × 1。
计算方法示例:
- 计算P(5, 3):表示从5个不同元素中取出3个元素进行排列。
- 计算5的阶乘:5! = 5 × 4 × 3 × 2 × 1 = 120。
- 计算(5-3)的阶乘:(5-3)! = 2! = 2 × 1 = 2。
- 最后计算P(5, 3) = 5! / (5-3)! = 120 / 2 = 60。
- P(5, 3) = 60。
三、组合公式及其计算方法
组合公式为:C(n, m) = n! / [m! × (n - m)!]。
计算方法示例:
- 计算C(7, 4):表示从7个不同元素中取出4个元素进行组合。
- 计算7的阶乘:7! = 7 × 6 × 5 × 4 × 3 × 2 × 1 = 5040。
- 计算4的阶乘:4! = 4 × 3 × 2 × 1 = 24,同时计算(7-4)! = 3!,但这里我们直接用4!来简化计算:C(7, 4) = 7! / (4! × 3!) = (7 × 6) / (1 × 2) = 42 / 2 = 21,但更严谨的步骤是先算出3! = 6,再算出C(7, 4) = (7 × 6) / (4 × 3) = 21。
- C(7, 4) = 21。
四、简化计算技巧
对于较大的n和m值,直接计算阶乘可能会导致较大的数字处理难度和精度问题,介绍几种简化的计算技巧:
1、递归法:利用组合数的递推关系C(n, m) = C(n-1, m-1) + C(n-1, m),从较小的m值开始逐步计算到m=n,这种方法特别适合于编程实现和手动计算较小的数值。
2、帕斯卡三角形(Pascal's Triangle):帕斯卡三角形是一个数学上的三角形阵列,其中每一行表示组合数C(n, m),通过查找帕斯卡三角形中的特定位置,可以直接得到C(n, m)的值,而无需进行复杂的计算,这种方法在编程和手动计算中都非常高效。
3、使用公式简化:对于C(n, m),当m接近n/2时,C(n, m)通常取得最大值,且C(n, m)与C(n, n-m)相等(即对称性),利用这些性质可以简化某些问题的计算过程。
五、实际应用案例
案例一:选课问题
一个大学里有8门不同的课程,学生需要从中选择3门课程进行学习,问有多少种不同的选课方式?
解:这是一个典型的组合问题,应用C(8, 3)来计算,C(8, 3) = 8! / [3! × (8-3)!] = 56种不同的选课方式。
案例二:密码组合问题
一个密码锁有3个转盘,每个转盘上有10个刻度(0-9),问这个密码锁有多少种不同的密码组合?
解:这是一个排列问题,因为密码的顺序很重要(即“123”和“321”是两种不同的密码),应用P(10, 3)来计算,P(10, 3) = 10! / (10-3)! = 10 × 9 × 8 = 720种不同的密码组合。
六、进阶应用与挑战
在更复杂的实际问题中,排列组合的应用往往需要结合其他数学知识进行综合分析,例如在统计学中,利用排列组合可以计算不同事件发生的概率;在计算机科学中,它可以用于算法设计中的状态转移和路径规划等,对于一些特殊的排列组合问题(如带限制条件的排列组合),可能需要采用更高级的数学工具或编程技术来求解。
排列组合公式的计算方法是数学中一项重要的技能,它不仅能帮助我们解决各种实际问题,还能加深我们对数学逻辑和结构的理解,通过本文的介绍,我们了解了排列组合的基本概念、公式的推导、简化计算技巧以及在实际问题中的应用,希望读者能够掌握这些知识,并在未来的学习和工作中灵活运用,对于更深入的探索和挑战性问题,建议进一步学习相关领域的专业书籍和文献,以拓宽自己的知识面和解决问题的能力。

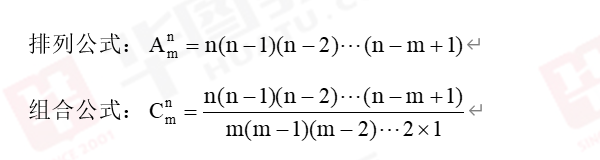
 京公网安备11000000000001号
京公网安备11000000000001号 鲁ICP备16005522号-2
鲁ICP备16005522号-2